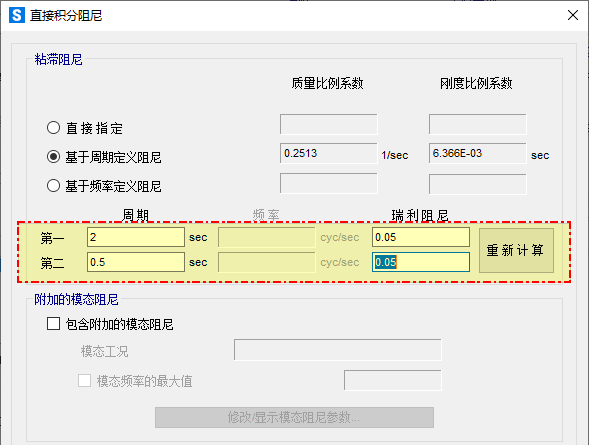
问题描述:
直接积分法的时程分析采用的瑞利阻尼有什么含义,该如何指定?
解答:
瑞利阻尼(Rayleigh)是目前地震响应分析中最常采用的阻尼模型之一,在 SAP2000 和 ETABS 中采用直接积分法做时程分析时,可以直接通过瑞利阻尼定义结构的阻尼大小。
瑞利阻尼由两部分构成:一项与质量矩阵成正比,一项与刚度矩阵成正比,其表达式为:

其中:[CM]=α0[M],[CK]=α1[K]。相应地,阻尼比也分为两项组成:与质量矩阵成正比项和与刚度矩阵成正比项,

其中:ξM=α0/2ωn,ξM=α1ωn/2
确定两个频率点 ωi 和 ωj 及其对应的阻尼比 ξi 和 ξj 就可以求解瑞利阻尼的比例系数 α0 和 α1。给定比例系数 α0 和 α1 后,可以看到阻尼 ξM 和 ξK 仅与 ωn 有关。下图给出了阻尼比随频率的变化规律曲线。
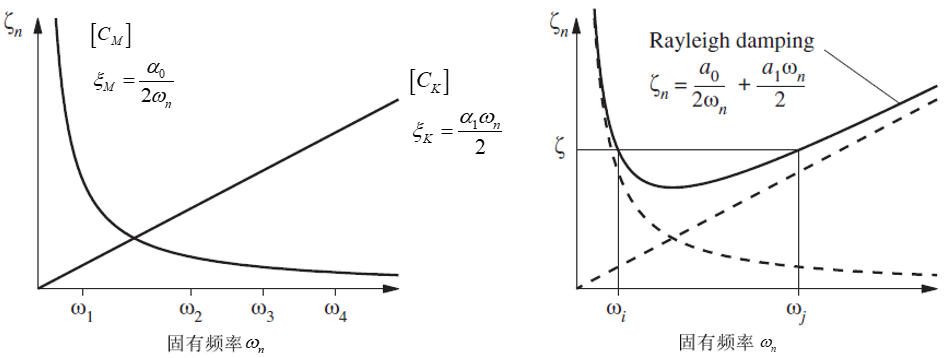
由上图可知,当结构频率趋近于 0 时,与质量相关的阻尼值 ξM 将会变得无穷大,而与刚度相关的阻尼 ξK 接近于0。质量阻尼 ξM 随着频率的增加而迅速变小,刚度阻尼 ξK 则与频率成正比,则随着频率的增加而线性增加。当频率趋近于无穷大时,刚度阻尼 ξK 同时趋近于无穷大,而质量阻尼 ξM 则趋近于无穷小。
在定义瑞利(Rayleigh)阻尼时,不能随意选取频率点 ωi 及其对应的阻尼比确定比例系数。当结构的振动频率在区间 [ωi,ωj] 之内时,结构的阻尼比将略小于给定阻尼比,结构的反应将略大于实际的反应,这样的计算结果对工程而言是安全的。而当频率在 [ωi,ωj] 区间之外时,其阻尼比均大于给定阻尼比,而且距离该区间越远,阻尼比越大。区间频率之外的振动反应会被抑制,其计算值将远远小于实际值。通常来说区间频率之外一部分是不需要考虑的,或可以忽略的,但是,如果存在对结构设计有重要影响的频率分量,则可能导致严重的不安全。
依据 CSI 的建议,瑞利阻尼可以通过指定结构的周期来定义。其中,第一周期可以取为 0.9T1,第二周期取 0.2T1(取 0.9T1 而非 T1 是为了防止阻尼偏小过多)。另外,也有建议第一周期取相应地震方向的第一阶周期,第二周期取质量参与系数达到 90% 时的振型周期
,这样算出来位移会偏大,因为阻尼比普遍偏小。对于这两个周期(或频率)的取值,用户应谨慎填写。必要的情况下,应调整周期的取值,查看结构的响应对其是否敏感。